Stepwise Regression with Minitab

What is Stepwise Regression?

Stepwise regression is a statistical method to automatically select regression models with the best sets of predictive variables from a large set of potential variables. There are different statistical methods used in stepwise regression to evaluate the potential variables in the model:

[unordered_list style=”star”]

• F-test
• T-test
• R-square
• AIC

[/unordered_list]

Three Approaches to Stepwise Regression

[unordered_list style=”star”]

• Forward Selection
  Bring in potential predictors one by one and keep them if they have significant impact on improving the model.
• Backward Selection
  Try out potential predictors one by one and eliminate them if they are insignificant to improve the fit.
• Mixed Selection
  Is a combination of both forward selection and backward selection. Add and remove variables based on pre-defined significance threshold levels.

[/unordered_list]

How to Use Minitab to Run a Stepwise Regression

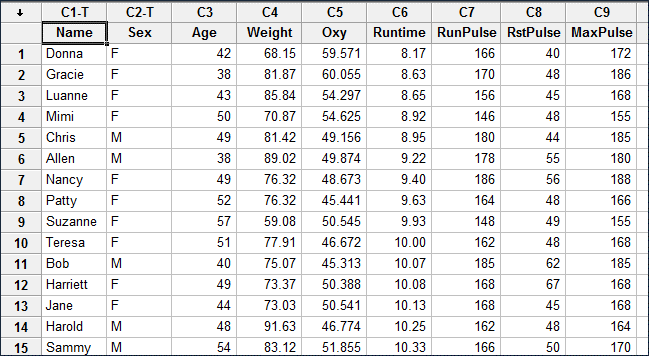
Case study: We want to build a regression model to predict the oxygen uptake of a person who runs 1.5 miles. The potential predictors are:

[unordered_list style=”star”]

• Age
• Weight
• Runtime
• Runpulse
• RstPulse
• MaxPulse

[/unordered_list]

Data File: “Stepwise Regression” tab in “Sample Data.xlsx”

Sample Data Glance

Steps to run stepwise regression in Minitab:

1. Click Stat → Regression → Regression → Fit Regression Model
2. A new window named “Regression” appears.
3. Select “Oxy” as the “Responses” and select all the other variables into the “Continuous Predictors” box.
   
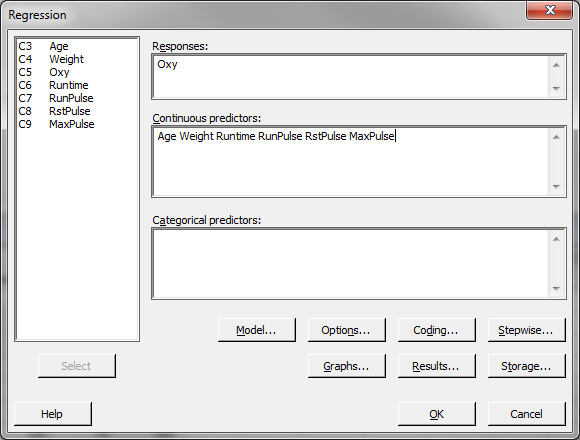
4. Click the “Stepwise” button and a new window named “Regression: Stepwise” pops up.
5. Select the method of stepwise regression and enter the alphas to enter/remove. In this example, we use the “Forward selection” method and the alpha to enter is 0.25.
   
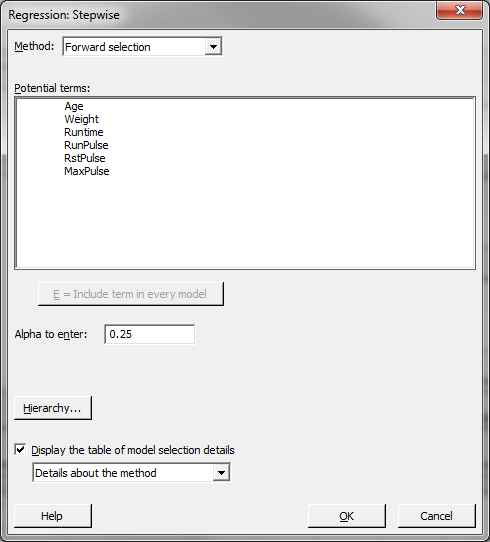
6. Click “OK” in the window “Stepwise – Methods.”
7. Click “OK” in the window “Stepwise Regression.”
8. The results appear in the session window.
   

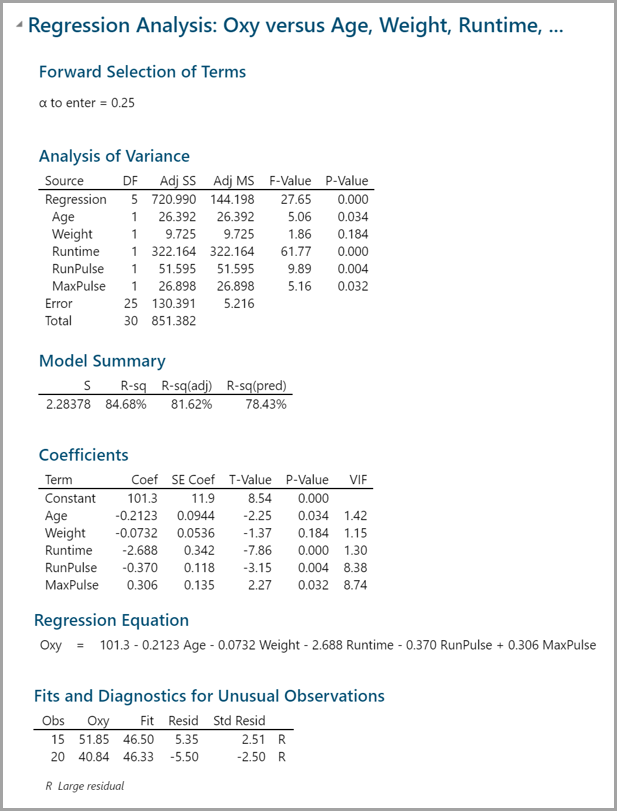
Model summary: One out of six potential factors is not statistically significant since its p-value is higher than the alpha to enter. Step History: Step-by-step records on how to come up with the final model. Each column indicates the model built in each step.